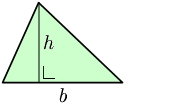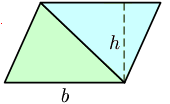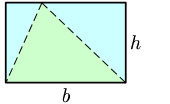
- La superficie de un triángulo se obtiene multiplicando la base por la altura (donde la altura es un segmento perpendicular que parte de la base hasta llegar al vértice opuesto) y dividiendo en dos. Siendo b la longitud de cualquiera de los lados del triángulo y h la distancia perpendicular entre la base y el vértice opuesto a esa base la superficie S queda expresada del siguiente modo:
- Si conocemos las longitudes de los lados del triángulo (a, b, c) es posible calcular la superficie empleando la fórmula de Herón.
donde p = ½ (a + b + c) es el semiperímetro del triángulo.
Cuando el triángulo es muy "afilado" (la suma de los dos lados menores es muy similar al valor del lado mayor) la fórmula anterior es inestable numéricamente).
Rescribiendo la fórmula anterior obtenemos: (suponiendo
a ≥ b ≥ c )
Otra forma de calcular el área es:
donde a y b son dos lados cuales quiera del triangulo y C es el ángulo comprendido entre ellos.
- La superficie de un triángulo se obtiene multiplicando la base por la altura (donde la altura es un
"A mis profesores, compañeros de trabajo, amigos... ...y todos aquellos que hicieron posible la confección y elaboración de este trabajo." |
La geometría es una ciencia del conocimiento del ser, pero no de lo que está sujeto a la generación y a la muerte. La geometría es una ciencia de lo que siempre es. Platón |